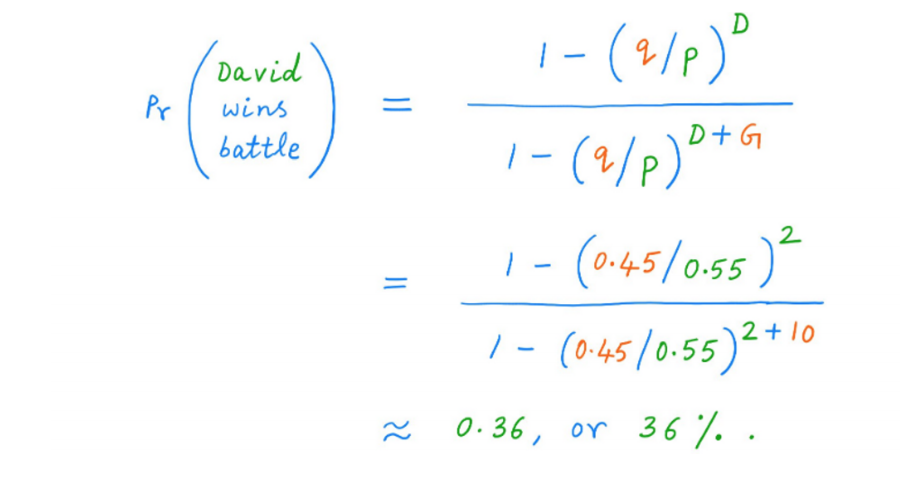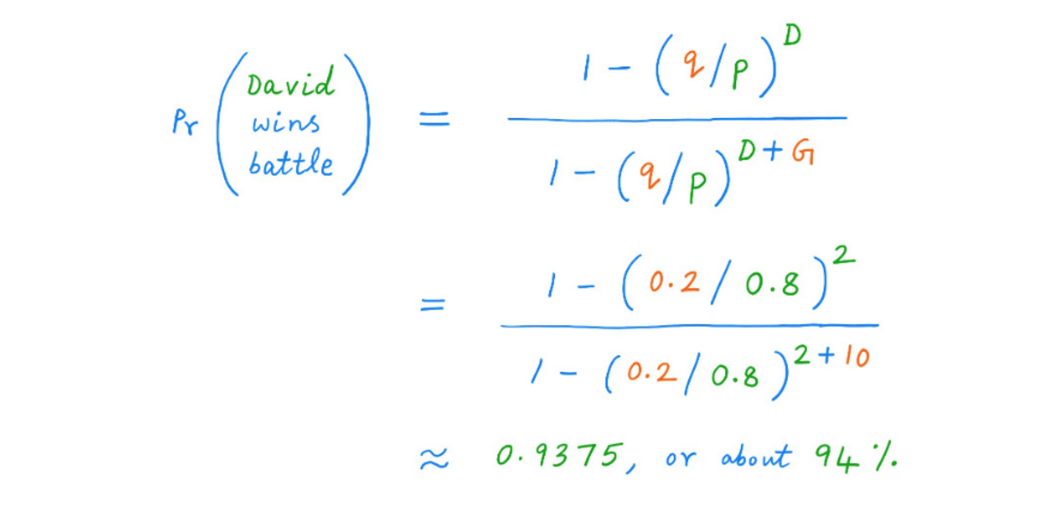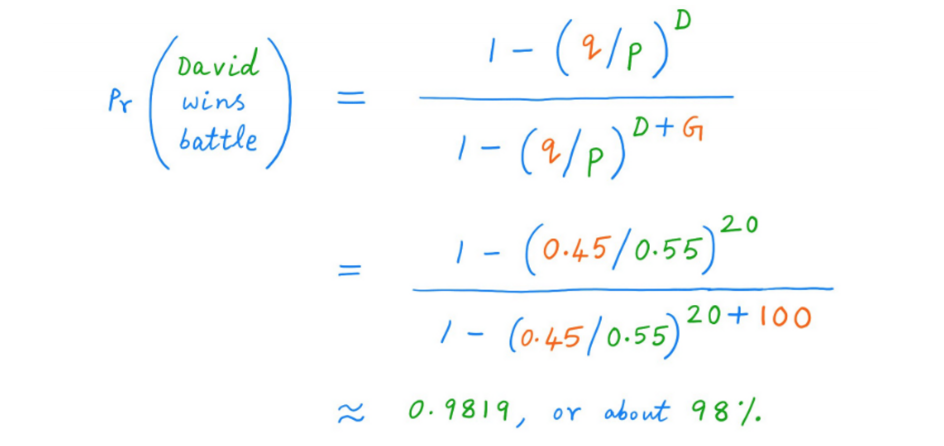22.02.24
Банкрутство азартного гравця
10 хвилин
1. У цій статті я розкажу вам про "Розгром азартного гравця". Це класична вправа в теорії ймовірностей. Але якщо не обмежуватися математикою, ця вправа може багато навчити нас у житті, бізнесі та інвестуванні.
2. На мій погляд, Розгром азартного гравця - це математика ситуацій типу "Давид проти Голіафа" ("Майстерність проти Розміру"). Тут Давид - "маленький" гравець. У нього обмежені ресурси. Але він дуже вмілий та досвідчений. Проти Давида виступає Голіаф - "великий" гравець, у якого більше ресурсів, але менше майстерності.
3. Битва між Давидом та Голіафом триває протягом кількох "раундів". В кожному раунді є "переможець" - або Давид, або Голіаф. Давид, завдяки своїй майстерності, має більшу ймовірність перемоги у кожному окремому раунді. У цьому перевага Давида перед Голіафом.
4. Але через асиметрію розмірів гравців, програш раунду впливає на Давида більш негативно, ніж на Голіафа. Іншими словами: Оскільки у Голіафа більше ресурсів, він здатний витримати більше ударів, ніж Давид. У цьому перевага Голіафа.
5. Це працює таким чином: Після кожного раунду переможений віддає переможцю частину своїх ресурсів. Так продовжується до тих пір, поки один з гравців не буде знищений, тобто у нього не залишиться ресурсів.
6. Розглянемо приклад. Припустимо, Давид приносить на стіл $2000. А Голіаф приносить $10000. Отже, на початку гри банкролл Голіафа в 5 разів більше банкролла Давида. Це і є перевага Голіафа в "розмірі".
7. Але на відміну від цього у Давида є перевага в "мастерності". Скажімо, це дає Давиду 55% шансів на перемогу в будь-якому раунді - порівняно з 45% у Голіафа.
8. І ми скажемо, що кожен раунд обходиться програвшому в $1000, які додаються до банкроллу переможця. Використовуючи ці правила, ми бачимо, що Голіафу потрібно виграти на 2 раунди більше, ніж Давиду. Цього достатньо, щоб знищити $2000 Давида - розорити його та програти битву.
9. Але щоб Давид вийшов на перше місце, він повинен виграти на 10 раундів більше, ніж Голіаф. Тільки тоді Давид зможе відібрати у Голіафа $10000 та розорити його. Здавалося б, завдання не з легких. Але ми повинні пам'ятати: в кожному окремому раунді шанс перемоги на користь Давида 55 на 45.
10. Отже, хто з більшою ймовірністю переможе у цій битві: Давид чи Голіаф? Достатньо чи переваги "мастерності" Давида 55/45, щоб перевищити перевагу "розміру" Голіафа $10K/$2K? І взагалі, скільки майстерності потрібно аутсайдеру, щоб компенсувати перевагу в розмірі?
Це і є суть головоломки "Розорення гемблера".
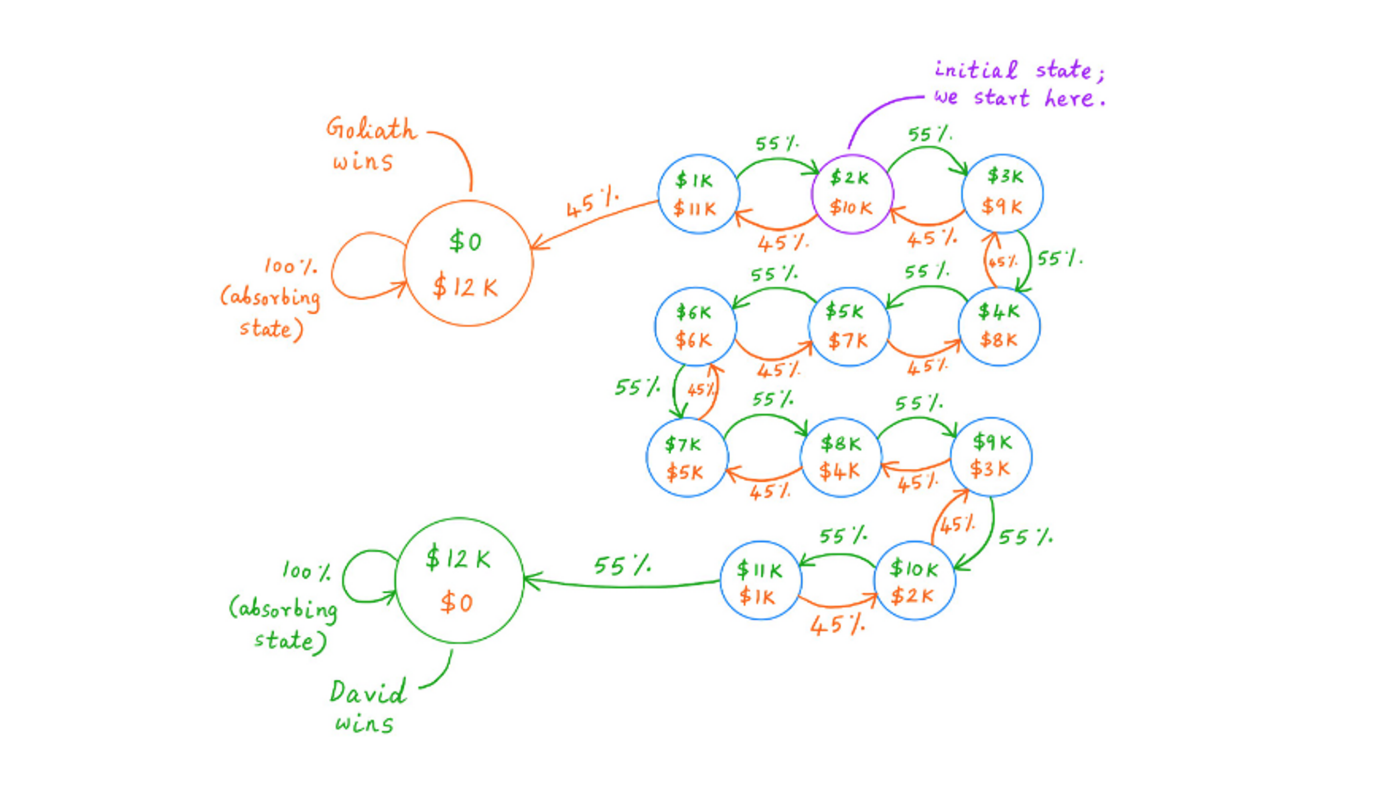
11. Ось зображення показує всі можливі варіанти подій, через які можуть пройти Давид і Голіаф, перш ніж один з них у кінці кінців переможе іншого.
Битва між Давидом і Голіафом може пройти через 13 можливих варіантів розвитку подій. Два з цих станів є "поглинаючими" - ми зупиняємося, коли досягаємо їх. Зелений поглинаючий стан - це коли Давид перемагає (після знищення Голіафа). А помаранчевий поглинаючий стан - це коли Голіаф перемагає (після того, як зробив Давида банкротом). У всіх 13 випадках зелені долари - це банкрол Давида, а помаранчеві долари - банкрол Голіафа. Битва починається в фіолетовому колі, де у Давида є $2K, а у Голіафа - $10K. У кожному не поглинаючому стані грається раунд, в якому перевага надається Давиду у співвідношенні 55 до 45. Після кожного раунду стан змінюється, відображаючи $1K, переданий програвшим - переможцю.
12. У математиків є спеціальна назва для такого типу зображень, заснованих на станах. Вони називають її ланцюгом Маркова. Ланцюги Маркова - це стандартна тема, вивчається в елементарних курсах теорії ймовірностей. Щоб дізнатися про них більше, дивись тут.
13. Існує безліч винахідливих способів аналізу ланцюгів Маркова. І один з таких способів дозволяє нам вирішити нашу головоломку "Розграбування гравця". Це дає нам формулу для розрахунку ймовірності перемоги Давида і Голіафа у битві:
Припустимо, що після кожного раунду програвший передає $k переможцю. Припустимо, що Давид починає з D*$k, а Голіаф - з G*$k. Отже, Давиду потрібно виграти на G раундів більше, ніж Голіафу, тоді як Голіафу потрібно виграти на D раундів більше, ніж Давиду. І нехай кожен раунд виграється Давидом з ймовірністю p, а Голіафом - з ймовірністю q = 1-p. За таких умов, ймовірність перемоги Давида у битві дорівнює:
Ймовірність перемоги Голіафа у битві = 1 мінус ймовірність перемоги Давида.
14. Застосовуючи цю формулу, ми бачимо, що у Давида лише ~36% шансів перемогти у цій битві - тобто шанси на користь Голіафа майже 2 до 1. Таким чином, перевага Давида у 55/45 "навичках" НЕ достатня, щоб протистояти перевазі Голіафа в $10K/$2K "розмірі", коли ставки становлять $1000/раунд.
У нашому прикладі маємо:
k = $1k (ставка на раунд),
D = 2 (Давид починає з $2K),
G = 10 (Голіаф починає з $10K),
P = 0,55 (так як Давид перемагає кожен раунд з ймовірністю 55%),
q = 0,45 (так як Голіаф перемагає кожен раунд з ймовірністю 45%).
Підставивши ці числа, ми отримуємо:
15. Для тих, хто хоче побачити, як ця формула розорення гравця виникає з наведеної вище ланцюга Маркова, ось математика. (Не хвилюйтеся, якщо ви не розумієте цієї математики. Я обіцяю, що вона вам не знадобиться до кінця цієї теми!)
16. Для мене "Розорення азартного гравця" - це не що інше, як просте математична вправа. Я вважаю, що вона може вчити нас принаймні 5 ключових уроків, що стосуються життя, бізнесу та інвестицій.
17. Ключовий урок 1: Життя має ймовірнісний характер. Тому ми повинні мислити у контексті ймовірностей, а не конкретними цифрами. Наприклад, припустимо, що майстерність Давида дає йому перевагу 80/20 над Голіафом. У такому випадку Давид майже завжди перевищує перевагу Голіафа у розмірах (~94% часу):
У нашому прикладі маємо:
k = $1k (ставка на раунд),
D = 2 (Давид починає з $2K),
G = 10 (Голіаф починає з $10K),
P = 0,8 — У Давида перевага над Голіафом в співвідношенні 80/20
q = 0,2
Підставивши ці числа, ми отримуємо:
18. Але навіть 94% шансів на перемогу - це НЕ перемога. Є все ще невеликий шанс, що Голіаф переможе Давида. Тому, якщо ми ставимо на перемогу Давида, ми повинні враховувати ці шанси. Наприклад, ми не повинні ставити всі наші гроші на Давида. Це було б ризиком розорення.
19. Ключовий урок 2: Коли ми протистоїмо комусь, хто має набагато більше ресурсів, ніж ми, ми повинні прагнути того, щоб шанси були на нашому боці. Якщо шанси дорівнюють 50/50, а у нашого противника безмежні глибокі кишені, ми безсумнівно програємо битву.
20. Фактично, це і є походження фрази "Ruina Gambler". Якщо азартний гравець з обмеженими ресурсами і відсутністю переваги продовжує грати проти казино з практично безмежніми ресурсами, то рано чи пізно він буде розорений. У таких ситуаціях будинок завжди виграє.
21. Ключовий урок 3: Експерименти з низькими витратами, як правило, підвищують шанси на перемогу. Наприклад, коли ставки складають $1000 за раунд, ми бачили, що перевага Голіафа у розмірі $10K/$2K дає йому шанси на перемогу майже 2 до 1, попри перевагу Давида у майстерності 55/45.
22. Але що, якщо ми зменшимо ставки до $100 за раунд замість $1000 за раунд, залишивши все інше без змін? Тепер шанси змінюються - у переважній більшості випадків на користь Давида. У кінцевому результаті він перемагає Голіафа у 98% випадків!
У нашому прикладі ми маємо:
k = $100 (ставка за раунд),
D = 2 (Давид починає з $2K),
G = 10 (Голіаф починає з $10K),
P = 0,8 — У Давида перевага над Голіафом у співвідношенні 80/20
q = 0,2.
Підставляючи ці числа, ми отримуємо:
23. Голіаф все ще має ТАКУ саму перевагу у розмірі $10K/$2K. І перевага Давида у майстерності також не покращилась. Вона все ще становить 55/45. Як же ймовірність перемоги Давида раптово зросла з ~36% до ~98%? У цьому і полягає сила того, що кожен раунд є експериментом з "низькою вартістю".
24. Бачите, коли кожен раунд коштував $1000, достатньо було 2 невдалих раундів, щоб перемогти Давида. Навіть при шансах 55/45 таке стається досить часто. Але коли кожен раунд коштує всього $100, потрібно принаймні 20 невдалих раундів, щоб розгромити Давида. При коефіцієнті 55/45 це дуже малоймовірно.
25. Такі люди, як: @JeffBezos, інтуїтивно розуміють силу таких низькозатратних ставок. Навіть якщо окрема ставка (наприклад, телефон Fire) виявиться невдачею, це малоймовірно призведе до банкрутства компанії. Фінансування багатьох таких низькозатратних ставок може бути дуже вигідним в довгостроковій перспективі.
З листа Безоса за 2018 рік:
“Невдачі теж потрібно масштабувати. При зростанні компанії все повинно масштабуватися, в тому числі і розмір вашіх невдалих експериментів. Якщо розмір ваших невдач не зростає, ви не будете створювати винаходи в такому розмірі, який дійсно може привести до успіху. Звісно, ми не будемо проводити такі експерименти легковажно. Ми будемо наполегливо працювати над тим, щоб зробити на них хороші ставки, але не всі хороші ставки в кінцевому підсумку окупаються. Таке масштабне прийняття ризиків є частиною послуг, які ми, як велика компанія, можемо надавати нашим клієнтам і суспільству. Гарною новиною для акціонерів є те, що одна велика виграшна ставка може з лихвою покрити вартість багатьох програшних. Розробка телефонів Fire і проекту Echo були розпочаті приблизно в один і той же час. Незважаючи на те, що телефон Fire виявився невдалим, ми змогли переняти наш досвід (а також досвід розробників) і прискорити наші зусилля по створенню Echo і Alexa. Ніхто з клієнтів не просив про Echo. Це визначено були наші ініціативи. Дослідження ринку не допомагають. Якщо б ви звернулися до покупця в 2013 році і сказали: "Хочете мати на кухні чорний, завжди увімкнений циліндр розміром з упаковку Pringles, з яким можна розмовляти і задавати питання, який також включає світло і відтворює музику?". Я гарантую, що вони б дивуватися подивилися на вас і відповіли: "Ні, дякую". З моменту появи першого покоління Echo, клієнти придбали більше 100 мільйонів пристроїв з підтримкою Alexa. ... і в 2018 році клієнти розмовляли з Alexa десятки мільярдів більше разів у порівнянні з 2017 роком.”
26. Ключовий урок 4: Віддавайте перевагу іграм з не нульовою сумою. Розорення азартного гравця, в суті, є грою з нульовим результатом. Кожен долар, який програв один гравець, виграв інший. У такій ситуації один з гравців у кінцевому підсумку буде розорений
27. Але що, якби кожен раунд був НЕ з нульовою сумою? Наприклад, що якщо переможець отримає $2, а програвший втратить лише $1? У таких випадках з "позитивною сумою" зазвичай є гарний шанс, що обидва гравці залишаться в живих на протязі невизначеного часу.
28. Отже, якщо кожен раунд має досить позитивну суму, навіть слабкий гравець - який знаходиться в невигідному положенні як за розміром, так і за навичками - може в кінцевому підсумку отримати високу ймовірність виживання і успіху протягом невизначеного часу. Тому, можливо, варто шукати та грати в такі нескінченні ігри.
29. Ключовий урок 5: Якщо ми протистоїмо сильному супернику, ми повинні з усіх сил намагатися зробити так, щоб він не зміг використати проти нас свою ПОВНУ силу. Gambler's Ruin - класичний приклад. Неважливо, чи є у Голіафа $1M. Якщо кожен раунд забирає лише $1K, решта $999K просто бездіяльні.
30. Давиду набагато краще грати з Голіафом по $1K за раз. Такий тип розрушення занадто часто зустрічається в бізнесі. Невеликі авангарди часто конкурують в ніші, яка не занадто турбує великих гравців. Закріпившись в цій ніші, новачок розвивається і стає серйозною загрозою.
31. Ось прекрасна стаття Джеймса Олворта (@jamesallworth), яка пояснює, як подібна ситуація склалася між Arm і Intel.
Рекомендовані теми
Кінець сторінки. Початок твого шляху
Поділіться своїми даними та очікуйте дзвінка протягом 24 годин. Ми відповімо на всі запитання та надамо ефективне рішення щодо ваших навчальних потреб.